Bridges Organization International Math and Art conference:
“Polarized and Dualistic Dimension Reversing Nature of the Cube and the Octahedron”
The Flexagon, a Bridge between the Polarized and Dualistic Dimension Reversing Nature of the Cube and the Octahedron
Abstract
In an attempt to understand the fundamental paradoxes of space and form and the working dynamics of parts and wholes, a set of underlying relational equations and formative architectural dualities became apparent. The following paper is an exploration of that relational geometry expressed as an embedded array of dual polytopes with increasingly concentric spheres of polar reciprocity, each defining the others dimensional perspective.
Synopsis: Geometrically, this underlying pattern looks like a nested array of embedded polygons whose edges define a set of increasingly concentric spheres through polar reciprocity. Additionally, there is a dimension reversing interaction between the levels of these concentric spheres that have interesting physical and metaphoric properties when expressed in form as generalized n-dimensional dual polytopes. The toroidal movement of this structure will be explored later in the paper as the initial 2D symbol is expressed in 3D and the mechanism of its movement can be explored. Ultimately, this will illustrate the flexahedron as a conversion bridge between the dual polytope expression of the cube and octahedron.
While metaphoric in nature, this symbol is potent in its ability to hold abstract and oftentimes paradoxical thoughts in harmony. Its aesthetic and mathematical properties may interest this conference and colleagues of math and art as it traverses dimensions and unfolds below. For inquiry, I have modeled out the perfect use case scenario where the Duality Gap between divergent layers has been set to 0.
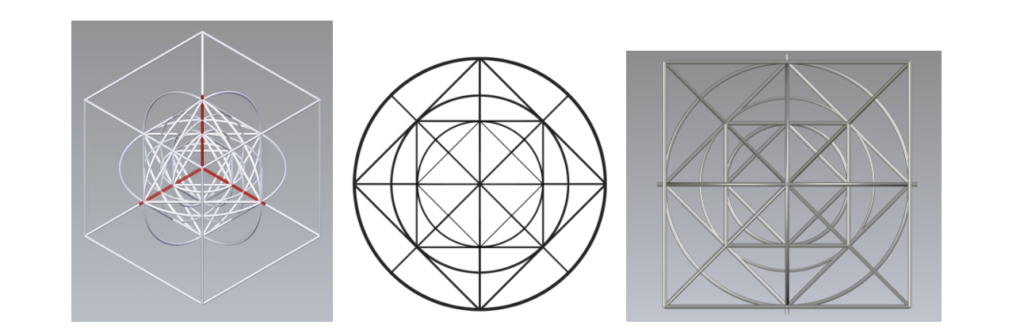(a) (b) (c)
Figure 1: Unifying Principle (a) 2D, (b) 3D Isometric View (c) 3D front view
Nested within the cube in figure 1 are both the concentric circles that define its inner and outer boundaries, as well as a dual octahedron that is formed in the negative space and edges of the cube. The dynamics of figure 1a illustrate a relationship of coherence, where the duality gap of apparent spheres is minimized allowing for the optimized number of embedded spheres to collectively emerge.
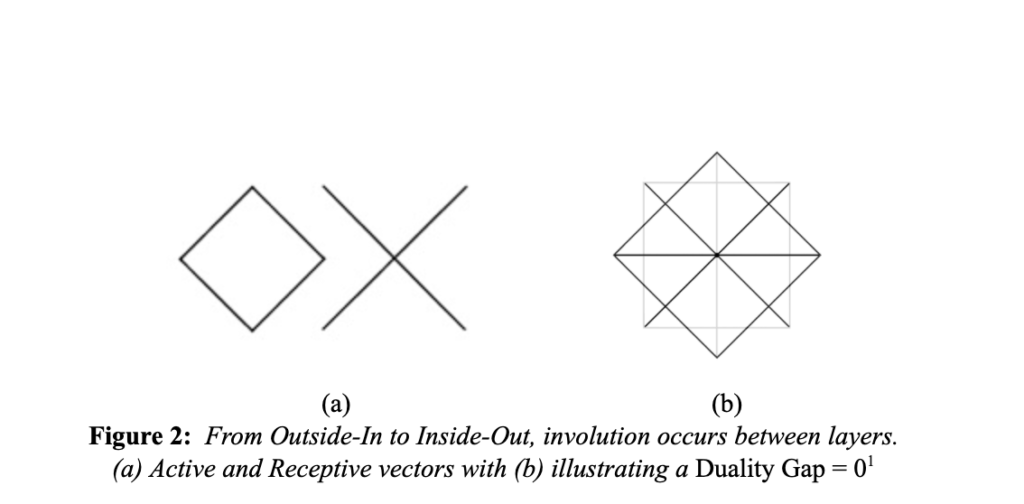
Representing the mechanics between and within the spheres, the 45-45-90 Isosceles Triangle emerges from a planar view as shown in figure 2b and forms the polygon faces that transform the spheres from one layer to the other. In the 2D, figure 1a, there are 16 isosceles triangles that will be used to construct the 3D printed flexahedron in figure 6. Two of these paired sides of will be used as concave and convex triangle pyramids to form the dual sided pairs of the tetrahedron with a hinge point/rod at their planar edges.
1 [1] In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. The solution to the dual problem provides a lower bound to the solution of the primal (minimization) problem. Their difference is called the duality gap.
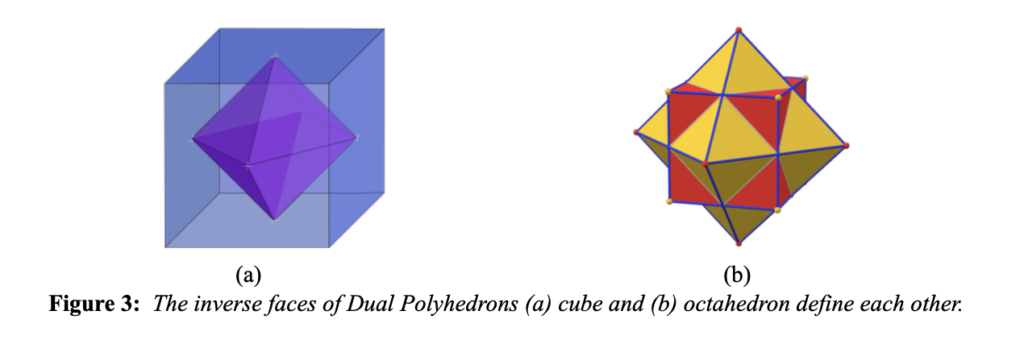
Geometrically this mathematical principle has been explored through the pairing of Dual Polyhedrons, where “the vertices of one shape correspond to the faces of the other, and the edges between pairs of vertices of one shape correspond to the edges between pairs and faces of the other.” [2] One defining the other in a co-creation of space and ultimately form.
What I find fascinating about this inquiry is not only it’s beauty and metaphoric power to explain the nature of duality, but also the physical mechanics and confines of its structure once constructed. I continued to see physical properties within the initial symbol that pointed to its ability and function to turn itself inside-out and outside-in.
Structurally, if the geometry of the 2D figure 1a is true, then the model should be able to find a way to turn itself inside out, along the polygon faces illustrated in 2a. Between the inner box and the outer box, the Initial Symbol seems to have both a cube and a torus, inverting itself from inside out and outside in. When modeling the initial symbol in 3D, this is exactly what we see…
Almost… Following the road of this simple geometry has been a challenging journey. It required transcoding a 2D symbol into a 3D model in order to understand the complexities of the polyhedrons it constructed; and then again translating that 3D model of perceived dual polyhedrons back into a flat 2D model so I could understand how the faces of the polygons tessellate with one another. All this so I could print a 3D model and confirm the mechanics and capacity for both involution and revolution between parts, i.e. concentric circles.[8]
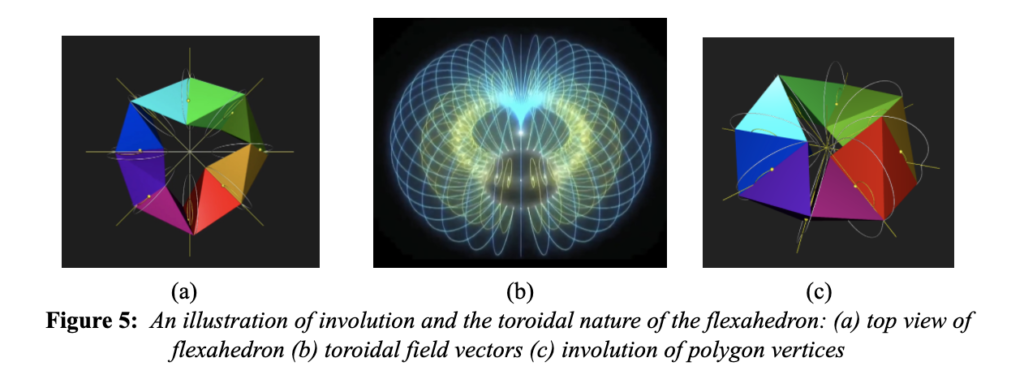
Staying with the geometry, Figure 5a below shows the structure of the proposed flexa-octahedron enfolding from outside/in while illustrating the vortex fields of its rotation in figure 5b. Notice in 5c the polarized concentric circles showing the toroidal fields vertices produced by each of the polygon edges. The vertex of each polygon transverses from the center radius to the outer edge of the figure and back in.
In order to print and see the underlying mechanisms and 3d structure of the 2d symbol in figure 1a, two base pair tetrahedrons are placed edge to edge with one another with a hinge between their edges. You can see this in the 8 tetrahedrons of the 3d model in figure 6a below, or the 16 isosceles triangle pyramids that are their polar half shells, as represented in figure 1a above.
Rather than print the model using solid tetrahedrons, I constructed each of them using two polarized sides that join together to form each of its four faces. This is important as it illustrates the phase shift in the final figure from one polarity to the next as it unfurls and will be useful in future application.
Strung together along the hinge points of their edges, two tetrahedrons come together to form their octahedron counterparts that is then connected with four other octahedrons forming a closed loop dual phase circuit.
Summary and Conclusions
Upon its construction, it was interesting to see two cubes of the same size go out of phase with one another and yet remain connected, occupying the same space and informing both the movement and structure of the other. In addition to the toroidal mechanics of its structure and unique expression of the polarized and dualistic dimension reversing nature of its form, I believe it’s worthy of follow-up inquiry.
So, what’s it do? That is the $1^10 question. Looking for funding or to join a research team and explore that together. Initial implications point to art, material sciences[4], fluid dynamics and system theory[5], consciousness research[6] and AI architecture[9], aerospace[3], encryption and data compression, quantum computing, awakening and singularity studies [6,7,8,9].
References:
[1] Wikipedia: Duality https://en.wikipedia.org/wiki/Duality_(mathematics)
[2] Wenninger (1983), Dual Models, C ambridge University Press, Oct 16, 2003
[3] Winfree (1987) When Time Slows Down P rinceton University Press
[4] Johannes Schonke, http://hannes.home.oist.jp/projects/babylon/kaleidocycles.html
[5] Geri, Michela et al. “Thermal Delay of Drop Coalescence.” Journal of Fluid Mechanics 833 (December 2017): R3 © 2017 Cambridge University Press
[6] Adyashanti – Entire discography of audio talks, https://www.adyashanti.org/
[7] Alan Watts – Entire discography of audio talks, https://www.alanwatts.org/
[8] Wilber (1996) Brief History of Everything, Shambhala Press
[9] Beck (1996) Spiral Dynamics, B lackwell Publishers
[10] Inspiration for constructing the 3d Octa-flexahedron: https://www.thingiverse.com/thing:3059727 [11] 2d/3d Flexahedron templates http://foldplay.com/kaleidocycle.action
Acknowledgements:
I want to offer a special thanks to Carlo Sequin for his guidance and encouragement to explore the geometric expressions behind this work and his video entitled Perfect Shapes in Higher Dimensions that inspired this paper.